La geometría, figuras en un plano o en el espacio

La geometría se ocupa del tamaño, la configuración y la posición de los
cuerpos en el plano o en el espacio. Tradicionalmente en la enseñanza de
Educación Primaria no se le ha dedicado mucho tiempo, lo que puede hacer que
parezca complicada para los niños y los adultos a pesar de que realmente
constituye una materia entretenida y amena que, aunque requiere cierto nivel de
abstracción, no ha de ser difícil para los más pequeños.
Para entrar en materia, primero
hay que conocer los conceptos de punto, línea, semirrecta, segmento, plano y
ángulos.
El punto es el concepto
geométrico más básico
Las líneas son ilimitadas
en los dos sentidos en que se pueden recorrer y se denotan mediante letras
minúsculas.
Si se dibuja una recta y en ella
se señala un punto la recta queda dividida en dos partes, cada una de las
cuales se denomina semirrecta.
Si dibujamos una semirrecta y en
ella señalamos dos puntos el fragmento comprendido es el segmento de
extremos.
El plano en geometría carece de grosor y es ilimitado en todas sus direcciones
BREVES
Las angulosas formas
Si dibujamos en un plano dos
semirrectas con un mismo origen, el plano queda dividido en dos partes, cada
una de las cuales recibe el nombre de ángulo o región angular. Existe gran
variedad de ángulos, pero los más característicos son el ángulo nulo, el recto,
el plano y el completo.
Cuando dos ángulos tienen el
vértice y un lado en común, se llaman consecutivos.
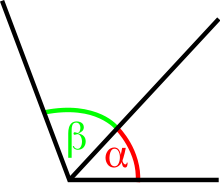
Si los lados no comunes de dos
ángulos consecutivos quedan sobre la misma recta se llaman adyacentes. Por lo
tanto, do ángulos adyacentes forman un ángulo plan

¡No confundas círculo con circunferencia!
La circunferencia es una línea
curva, cerrada y plana cuyos puntos equidistan de otro punto situado en
interior denominado centro. Mientras que el círculo son el conjunto de los
puntos del plano que distan del centro de una circunferencia una distancia
igual o menor que su radio, es decir, al conjunto de los puntos interiores de
la circunferencia.
El radio de la
circunferencia es un segmento que une el centro de esta con un punto cualquiera
de sus puntos.
La cuerda es el segmento
que une dos puntos cualesquiera de la circunferencia.
El arco es la parte de la circunferencia limitada por dos de sus puntos, denominados extremos del arco.
Un sector circular es la parte
del círculo limitada por un arco y por los radios que corresponden a sus
extremos.
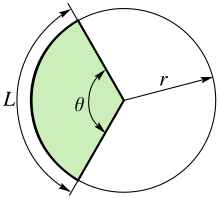
Un segmento circular es la parte
del círculo limitada por su arco y su cuerda
“Poligoneando”
Un polígono es un espacio limitado por una línea
quebrada, cerrada y simple. Los nombramos según el número de lados o vértices
que tienen. Nosotros vamos a estudiar los triángulos y los cuadriláteros.
Los triángulos
Podemos clasificarlos según las
longitudes de sus lados como; escalenos, en los que no coinciden la longitud de
ningún lado; isósceles, si tienen solo dos ángulos iguales-; y equiláteros, con
los tres lados iguales.
También los podemos clasificar
según sus ángulos; acutángulos, cuando sus tres ángulos son agudos;
rectángulos, cuando tienen un ángulo recto y los otros dos agudos; y
obtusángulos, cuando uno de sus ángulos es obtuso y los otros dos restantes
agudos.

Si desde un vértice de un
triángulo se traza la perpendicular del lado opuesto, el segmento que queda
comprendido entre el vértice y el lado es una altura del triángulo. Si trazamos
todas las alturas de un triángulo se cortan siempre en un único punto al que se
denomina ortocentro.

Las medianas son los segmentos que unen cada vértice con el punto medio del lado opuesto. Las medianas son siempre interiores. Se cortan en un único punto denominado baricentro.

Las mediatrices de un lado se definen como las rectas perpendiculares a dicho lado que pasan por su punto medio. Determinan el circuncentro, desde donde se traza la circunferencia circunscrita.

Las bisectriz de un ángulo es aquella línea que lo divide en dos ángulos tales que son exactamente iguales entre sí. Se cortan en el incentro.
Los cuadriláteros
Son figuras geométricas planas
con cuatro vértices, cuatro lados, cuatro ángulos y dos diagonales.
Un trapecio es un cuadrilátero
con dos lados paralelos tiene también paralelos lo otros dos es un
paralelogramo.
Si los cuatro ángulos son rectos
estamos ante un rectángulo.
Si los cuatro lados son iguales
es un rombo.
Cuando los lados son iguales y los
ángulos rectos tenemos un cuadrado.
PONTE A PRUEBA
Comprueba tus conocimientos geométricos en el siguiente enlace:
http://www.srbarreiro.es/mat2eso.html
EL PROFE PENSADOR
Sabemos que el ángulo inscrito es
igual a la mitad del ángulo central que determinan las rectas que van desde el
centro a los extremos del ángulo inscrito. Consideremos un círculo con centro O
que tiene inscrito un ángulo de 30 º. Determina cuánto valdrá el ángulo central
correspondiente.
SOLUCIÓN: Como el ángulo inscrito
es igual a la mitad del ángulo central correspondiente, si el ángulo inscrito
mide 30ª, el ángulo central medirá 60ª.
HACE MUCHO TIEMPO
Euclides es uno de los
matemáticos más importantes de todos los tiempos. En su obra Elementos propone diez afirmaciones o
postulados a partir de cuyos conceptos se demuestran una serie de teoremas que
constituyen lo que se conoce como geometría euclidiana. Muchos matemáticos han
estudiado los cinco postulados geométricos de esta obra para verificar que son
independientes, es decir, que ninguno se puede verificar a partir de los otros.
Durante mucho tiempo se sospechaba que el quinto, conocido como el postulado de
las paralelas no lo era, hasta que en el siglo XIX los matemáticos Lobatchevski
y Riemann propusieron dos variaciones distintas del quinto postulado que dieron
lugar a las geometrías no euclidianas, con propiedades diferentes a las
propuestas por Euclides pero con la misma validez desde el punto de vista
científico.
No hay comentarios:
Publicar un comentario