Profundizando un poquito en el espacio…
En
este tema hemos repasado los conceptos sobre longitud de perímetros, cálculo de
áreas, el teorema de Thales, el teorema de Pitágoras y también hemos hecho
ejercicios sobre pendientes. Daré un breve repaso a los contenidos principales
del tema.
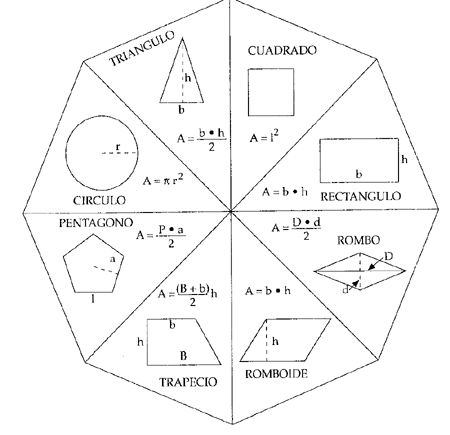
Para carcular el área de las
figuras geométricas más comunes como cuadrados, rectángulos, triángulos, etc.,
se utilizan distintas fórmulas matemáticas como, por ejemplo, multiplicar la
base por la altura en el caso del rectángulo. Todas estas fórmulas se basan en
la descomposición de la figura a la que se aplican en cuadrados unitarios
iguales, cuyo lado puede ser de un metro, un decímetro, un centímetro u otra
unidad, según convenga.
.gif)
Teorema de Pitágoras

Teorema de Thales

PONTE A PRUEBA
(Se incluye una página con ejercicios e información sobre las escalas)
http://mates-magicas.blogspot.com.es/2011/03/ejercicios-resueltos-de-tales-y.HTML
http://nuestrazonasextomatematicas.blogspot.com.es/2011/05/escalas-planos-y-mapas.HTML
http://www.profeperedo.cl/4%C2%BAmedio/areasyvolumenes/areas_volumen1.PDF
http://milagrotic.blogspot.com.es/2013/03/matematicas-6-la-escala-planos-y-mapas.html
CURIOSIDADES
El número pi es la relación entre
la longitud de una circunferencia y su diámetro. Es un número irracional, es
decir, que no existe ninguna fracción que dé exactamente su valor. Aunque se
han calculado varios millones de decimales de pi, para la mayoría de los
cálculos prácticos es suficiente con considerar dos o tres cifras decimales.
Calcular valores cada vez más exactos de pi ha sido una preocupación de los matemáticos de todas las épocas. Con 39 cifras decimales es suficiente para calcular la longitud de una circunferencia que abarcaría todo el universo conocido con un error menos que el radio de un átomo de hidrógeno. No obstante, el hombre sigue buscando más decimales de pi, aprovechando para ello cada nuevo avance que se realiza en el campo de la informática.
EL PROFE PENSADOR
El libro primero de Reyes dice:
“Después hizo un depósito de bronce fundido. De forma redonda, medía diez codos
de un extremo a otro y cinco codos de profundidad. Tenía treinta codos de
perímetro”. ¿Cuál es el valor de π que
se deduce de ese versículo de la Biblia?
SOLUCIÓN: Como π es la relación
entre el perímetro de una circunferencia (treinta codos) y su diámetro (diez
codos de un extremo a otro), tenemos que π . 5= 5.3. El valor de π en la Biblia
es 3.
No hay comentarios:
Publicar un comentario